BANGUN RUANG SISI DATAR (4) : PRISMA

-

 

Prisma

Perhatikan gambar berikut.

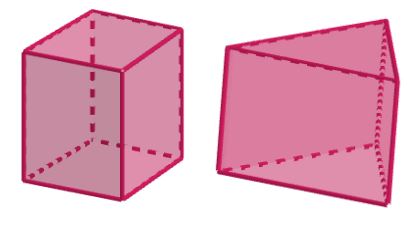
Prisma

Pada gambar tersebut terdapat dua bangun prisma.

Berdasarkan gambar tersebut, dapatkah kalian mendefinisikan apa itu prisma?

Prisma merupakan salah satu jenis bangun ruang yang dibatasi oleh sisi alas dan sisi tutup serta sisi-sisi tegak yang berbentuk persegi atau persegi panjang.

Dua gambar di atas merupakan bangun prisma segiempat dan prisma segitiga. Penamaan prisma tersebut berdasarkan bentuk alas dan tutupnya. Alas dan tutup prisma memiliki bentuk dan ukuran yang sama (kongruen).

Karakteristik prisma segi-n yaitu sebagai barikut.

  • Prisma memiliki n + 2 sisi. 2 sisi yaitu sisi alas dan sisi tutup serta n sisi tegak.
  • Banyaknya titik sudut pada prisma adalah 2n.
  • Prisma memiliki 3n rusuk, n rusuk pada sisi alas, n rusuk pada sisi tutup, dan n rusuk pada sisi tegak.

Selanjutnya akan dibahas mengenai penerapan prisma dalam kehidupan sehari-hari.


Jaring-Jaring Prisma

Perhatikan gambar berikut.

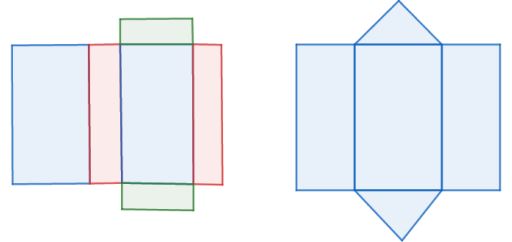
Jaring Jaring Prisma

Kedua jaring-jaring tersebut merupakan jaring-jaring prisma segiempat dan prisma segitiga. Selanjutnya akan dijelaskan mengenai rumus yang digunakan dalam menyelesaikan permasalahan terkait prisma.

Rumus Prisma

Rumus prisma yang akan dibahas yaitu rumus luas permukaan prisma dan rumus volume prisma.

Luas Permukaan Prisma

Perhatikan gambar berikut.

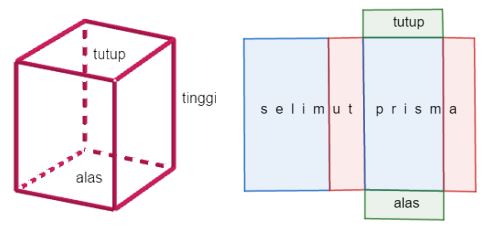
Luas Permukaan Prisma

Pada gambar tersebut terdapat bangun prisma dan jaring-jaring prisma. Prisma memiliki sisi alas, sisi tutup, dan sisi tegak (selimut prisma).

Untuk menentukan luas permukaan prisma dapat menghitung jumlah luas sisi-sisi prisma tersebut. Secara umum, untuk menghitung luas permukaan prisma yaitu

Rumus Luas Permukaan Prisma

Luas permukaan prisma = luas alas + luas tutup + luas sisi-sisi tegak

Karena alas dan tutup prisma memiliki bentuk dan ukuran yang sama, maka keduanya memiliki luas yang sama juga, sehingga

Luas permukaan prisma = 2 x luas alas + luas sisi-sisi tegak

Jika kita lihat sisi-sisi tegak (selimut prisma) dalam jaring-jaring di atas berbentuk persegi panjang, dengan panjangnya merupakan keliling alas prisma dan lebarnya merupakan tinggi prisma.

Lp = (2 x Lalas)+ (Kalas x t)

Keterangan:

  • Lp  : luas permukaan prisma
  • Lalas  : luas alas prisma
  • Kalas  : keliling alas prisma
  • t     : tinggi prisma

Berikutnya merupakan pembahasan mengenai volume prisma.

Volume Prisma

Perhatikan gambar berikut.

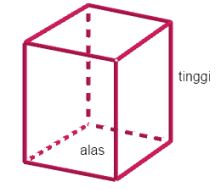
Volume Prisma

Perbedaan perhitungan balok dengan prisma terletak pada bentuk alas prisma. Jika pada balok alas berbentuk persegi panjang, dalam prisma alasnya memiliki bentuk yang lebih beragam, dapat berupa segitiga, segiempat, segilima, dan segibanyak lainnya.

Untuk menentukan volume prisma dapat dengan menggunakan rumus berikut.

Rumus Volume Prisma

V  = Lalas  x t

Keterangan:

  • V  : volume prisma
  • Lalas  : luas alas prisma
  • t    : tinggi prisma

Kerjakan latihan soal berikut untuk meningkatkan pemahamanmu mengenai prisma.

Contoh Soal Latihan Prisma

1. Tentukan banyaknya sisi, rusuk, dan titik sudut pada prisma segiduabelas.

Pembahasan

n = 12

Banyak sisi = n + 2 = 12 + 2 = 14 sisi

Banyak rusuk = 3n = 3 x 12 = 36 buah rusuk

Banyak titik sudut = 2n = 2 x 12 = 24 titik sudut

2. Suatu prisma segiempat memiliki alas berbentuk belah ketupat dengan ukuran diagonal-diagonalnya adalah 24 cm dan 10 cm. Jika tinggi prisma tersebut adalah 15 cm, tentukan luas permukaan prisma tersebut.

Pembahasan

Lalas = ½ x d1 x d2 = ½ x 24 cm x 10 cm = 120 cm2

Panjang sisi alas = √(122 + 52) = √(144 + 25) = √169 = 13 cm

Kalas = 4 x s = 4 x 13 cm = 52 cm

Lp = (2 x Lalas)+ (Kalas x t)

= (2 x 120 cm2) + ( 52 cm x 15 cm)

= 240 cm2 + 780 cm2 = 1020 cm2

3. Suatu prisma segiemapt memiliki alas berbentuk trapesium dengan ukuran panjang sisi-sisi sejajarnya 4 cm dan 8 cm serta tinggi trapesium adalah 10 cm. Jika tinggi prisma adalah 20 cm, tentukan volume prisma segiempat tersebut.

Pembahasan

Lalas  = ½ x (a + b) x t = ½ x (4 + 8 ) x 10 = 60 cm2

V  = Lalas  x t

= 60 cm2 x 20 cm = 1200 cm3

Comments

Post a Comment

Popular posts from this blog

KOORDINAT KARTESIUS (1) : TITIK KOORDINAT, POSISI TITIK PADA KOORDINAT KARTESIUS, POSISI TITIK TERHADAP SUMBU KOORDINAT

-
Image
 KOORDINAT KARTESIUS     Koordinat kartesius adalah sistem yang menerapkan setiap titik di bidang koordinat. Seperti ini gambar koordinat kartesius     Pada koordinat kartesius, terdapat 2 sumbu, yaitu sumbu x atau biasa disebut absis dan s umbu y yang disebut ordinat. Titik tengah (0,0) disebut titik asal.           Pada koordinat kartesius, kita menyebut posisi suatu titik terhadap jaraknya terhadap sumbu x dan sumbu y. Penyebutan atau penulisannya disebutkan terlebih dahulu sumbu x nya kemudian sumbu y. Sebagai contoh pada gambar di atas ketika ditarik garis, maka titik A berada pada angka -3 pada sumbu x dan berada pada angka 4 pada sumbu y. artinya titik A memiliki koordinat (-3, 4). Contoh Koordinat titik-titik diatas adalah .... A(6, 3) B(6, -1) C(-3, -2) D(-6, 4) E(3, -6) F(-7, -4)     Koordinat kartesius dibagi menjadi 4 bagaian yang dinamakan kuadran, beginilah pembagian kuadran pada koordinat kartesius Pada k...
Read more

PELUANG (2) : PERCOBAAN, RUANG SAMPEL, DAN TITIK SAMPEL

-
Image
PERCOBAAN, RUANG SAMPEL, DAN TITIK SAMPEL Anak-anak kelas 8 Grisaka pernah   bermain permainan ular tangga? Sebelum kamu punya kesempatan melangkah, permainan mengharuskan kita melempar dadu.  Nah , saat melempar, kemungkinan mata dadu yang muncul adalah 1, 2, 3, 4, 5 atau 6.  Pelemparan dadu seperti ini merupakan contoh dari percobaan , yang merupakan salah satu materi peluang dalam matematika. Untuk lebih lengkapnya, baca sampai habis ya! Kemunculan mata dadu 1, 2, 3, 4, 5 atau 6 jika dihimpun maka diperoleh himpunan {1,2,3,4,5,6}.  Himpunan disebut juga dengan   ruang sampel.  Nah,  sebenarnya ada lagi yang disebut sebagai  titik sampel.  Hubungan antara percobaan, ruang sampel, dan titik sampel tersebut akan kita bahas satu-persatu.    1. Pengertian Percobaan, Ruang Sampel, dan Titik Sampel Percobaan  atau eksperimen, yaitu suatu kegiatan yang dapat memberikan beberapa kemungkinan. Contoh: Melemparkan dadu, melemparkan koin...
Read more

LINGKARAN 3 : HUBUNGAN SUDUT PUSAT DAN SUDUT KELILING

-
Image
  Pengertian Sudut Pusat dan Sudut Keliling Sudut Pusat merupakan sudut yang dibentuk oleh dua jari-jari dan berbentuk pada inti lingkaran. (Lihat gambar: 1). Sudut Keliling merupakan sudut yang dibentuk oleh dua tali busur yang berbentuk di satu titik pada keliling lingkaran. (Lihat gambar: 2) Gambar 1 – Sudut Pusat Gambar 2 – Sudut Keliling Hubungan Antara Sudut Pusat dan Sudut Keliling Perhatikan pada gambar diatas, bawah sudut AOB adalah sudut pusat dan sudut ACB merupakan sudut keliling yang menghadap busur yang sama yaitu busur AB. Kita akan mempelajari hubungan antara sudut pusat dan sudut keliling yang menghadap busur yang sama. Lingkaran di samping memiliki jari-jari OA, OB, OC, OD = r Misal : sudut AOD = x dan sudut DOB = y, maka besar sudut AOB = sudut AOD + sudut DOB = x + y Perhatikan Segitiga BOC! Sudut BOC pelurus bagi sudut DOB maka sudut BOC + sudut DOB = 180°, sehingga sudut BOC = 180° – sudut DOB = 180° – y. Segitiga BOC adalah segitiga kaki, karena OC dan OB ada...
Read more